It’s time to introduce your class to the subject of division. You teach the vocabulary of division and then you begin problem-solving. Yet, when you problem solve, do you teach just one type of division problems or do you teach both? Most often teachers will introduce students to one kind and never even mention the other.

It’s quite common among teachers to introduce students to fair sharing. This is technically called Partitive division. However, the common core standards require us to teach both partitive and quotative division. Quotative division is creating sets–and often overlooked.
Teaching Partitive Division (or Fair Sharing)
While fair sharing division doesn’t need much introduction, I’ll still provide information about it so this post is complete. First, fair sharing is often “taught” to children before it’s formally taught in the classroom during math. For instance, my twins are five and they definitely can tell you about fair sharing when it comes to cookies, candy, and other things they want.
Fair sharing is essentially just repeated subtraction. Students simply take the dividend and evenly distribute it among the divisor. This is typically done in a concrete matter first, whether with base-ten blocks, goldfish crackers, or the like. Then, students should be moved into the semi-concrete, and finally into the abstract. You can read about how to teach math so students get it here. (See image below.)

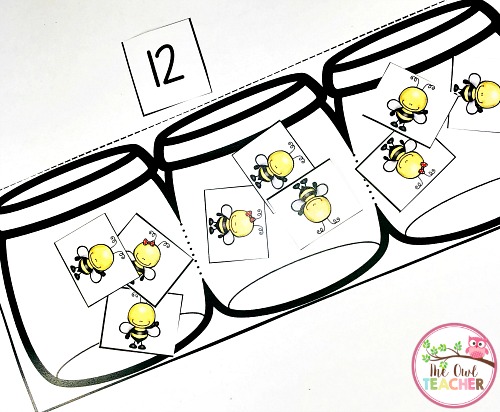
In class, you would have students sort things into groups such as this activity below, where we sort bees into jars. In partitive division, the question would look like this:
You have 12 bees that need to be sorted evenly into 3 jars. How many bees will you place into each jar?
In this problem, the dividend is known (the 12 – total number of bees) and the number of groups is known (the divisor as the jars), but the number in each group is unknown until the problem is solved. (And the problem below is not completed. There are more bees off in the corner, but the image is cut off.)
Teaching Quotative Division (Measurement)
Quotative division is the least taught–especially at the concrete level. Just as in multiplication, this is the “sets” version. Just as in the partitive type, the student is told the total number of items, and then they need to divide the sets into groups. However, the number of the groups is not known. They only know how many are in each group.
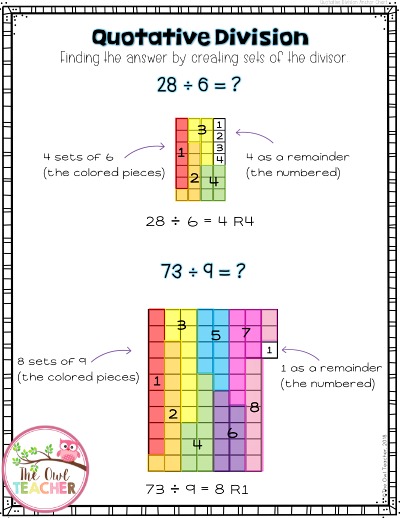
When I teach my students to do this, I pull out graphing paper and color pencils. I do not worry about arrays. I don’t feel that is our focus at this time. First, I have students either cut out the dividend or outline it in heavy black. Then I have students color in each set, or the divisor, in a different color until they have completed the graphing paper or until they cannot complete anymore sets. We then discuss if there is a remainder or not. (See the chart above.)
As in the example above, in quotative division the problem would look like this:
You have 12 bees. You are going to put them in jars, with 3 in each jar. How many jars will you need?
Again, in this problem, the dividend is known (the total number of bees – 12), the number in each group is known (the sets – divisor of 3), but the number of groups is unknown.
And using the method of graph paper and color pencils that I use, it would look like this below:

We then took all of these together and created a quotative division craftivity to hang up and display. (See image below.)

Grab Your FREEBIE!
I decided that since quotative division is the least concrete taught type, I would provide you with a free lesson that has all of the materials in this post. It includes the step-by-step lesson on how to teach it (in the math workshop format, but you can modify it to your liking), along with the independent activity that includes the craftivity. It also includes the anchor chart above. It is a small sample from my fourth-grade division math workshop (or you can find it on TpT here).
Grab your FREE division activity by clicking here.