
Math is very important. Even without all the standardized testing, we know that it’s critical for students to grasp it. Unfortunately, there are some students who struggle everyday with math and just loathe it. What are some ways we can work on teaching math so students get it?

If you want students to have a deeper understanding of math and make connections between what they already know and what’s new, it’s best to teach each math concept using the CRA method. This method helps blend the conceptual and procedural concepts of math all while working students through the gradual release of responsibility. I have found extreme success using this methodology.
What is the CRA Method?
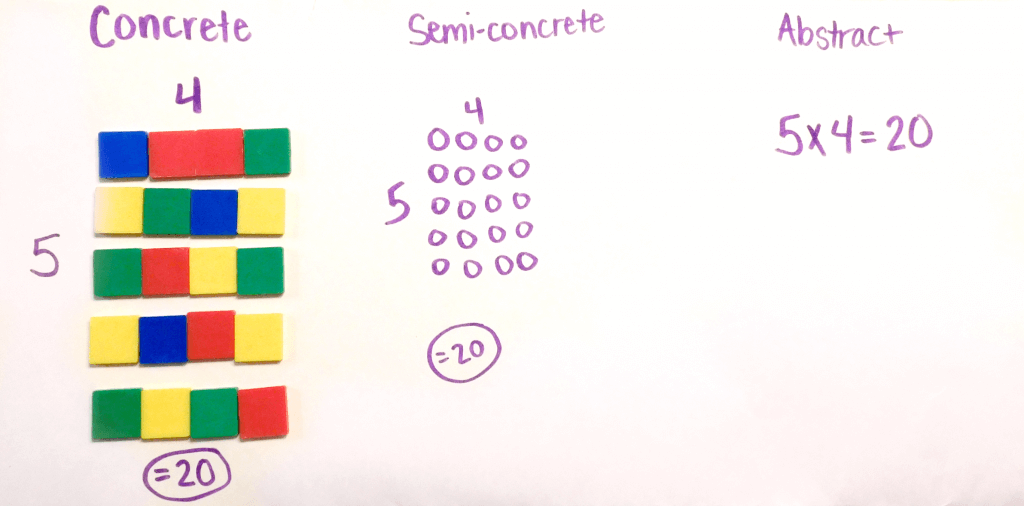
Concrete
The first step to every math concept that you introduce to students is making sure that you are making it concrete. When you are making math concepts concrete, you are pulling out the hands-on materials or manipulatives. This is the “doing” process of math. As with any new concepts, teachers should always describe and model what they are doing.
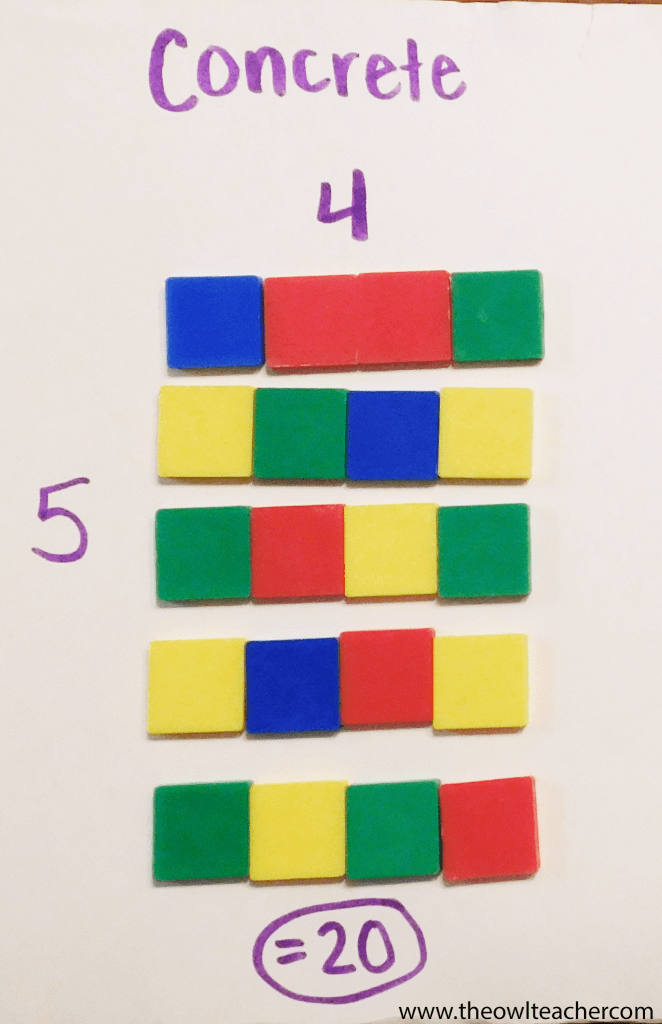
Representational
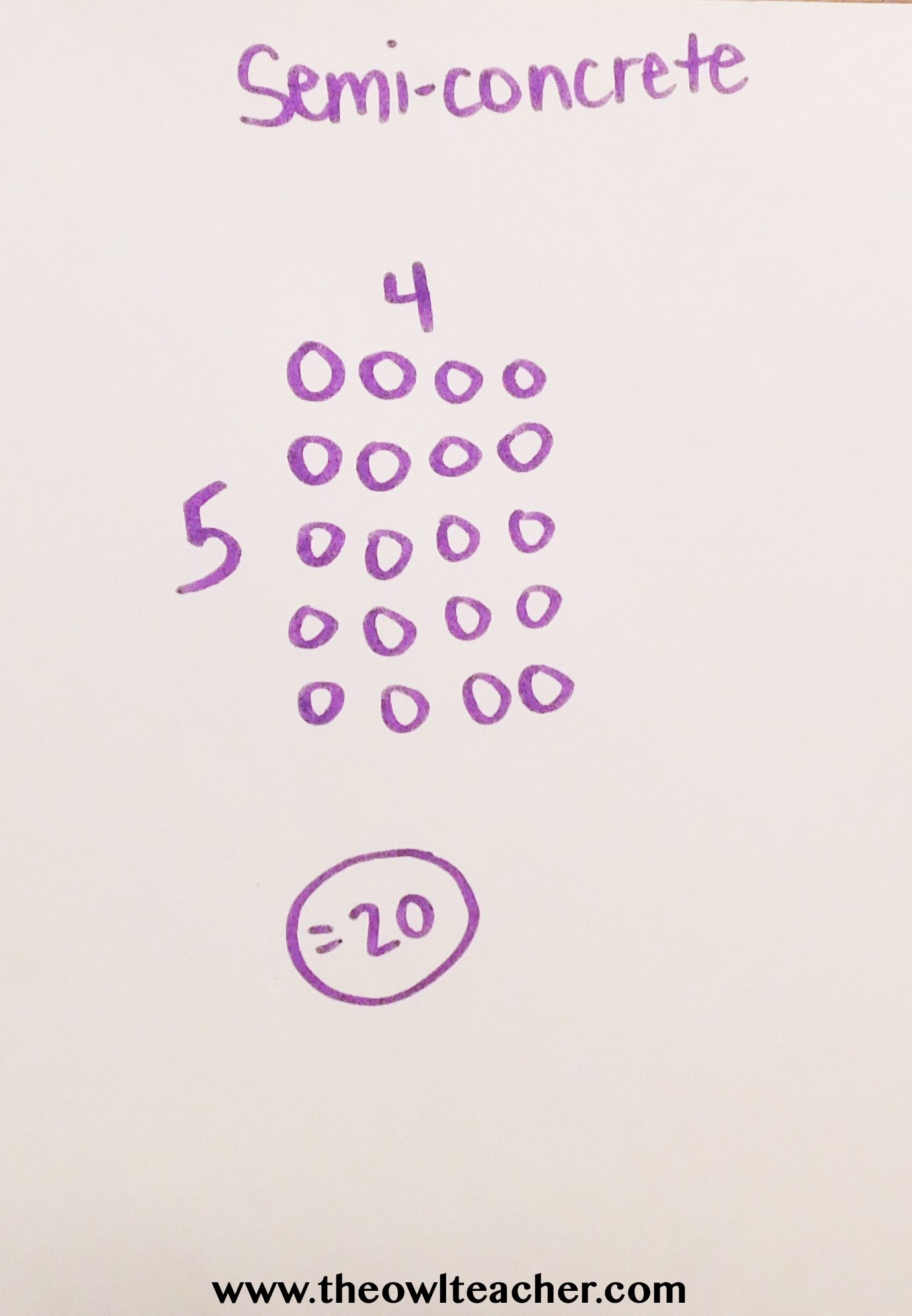
The next step to the CRA Method is called Representational. However, when I was in college, we called it Semi-Concrete, so I still tend to refer to it like this. This step follows the concrete step and moves students one step closer to the type of math most of us are familiar with – paper and pencil. Instead of providing students with manipulatives, we hand them a piece of paper and a pencil and have them draw (or represent) the manipulatives. Instead of having a student create an array of five groups of four using the manipulatives of tiles, we have students draw the array out. This is referred to as the “seeing” process.
Abstract
Unfortunately, many teachers will skip the previous processes because it can be time-consuming, but it is absolutely critical for a student to understand the abstract step. This step is where students are exposed only to the numbers and symbols in math. Using the example above, here students would only solve the multiplication equation of 5 x 4 = 20. Without the previous steps, students would likely not understand the why or how of the concept.
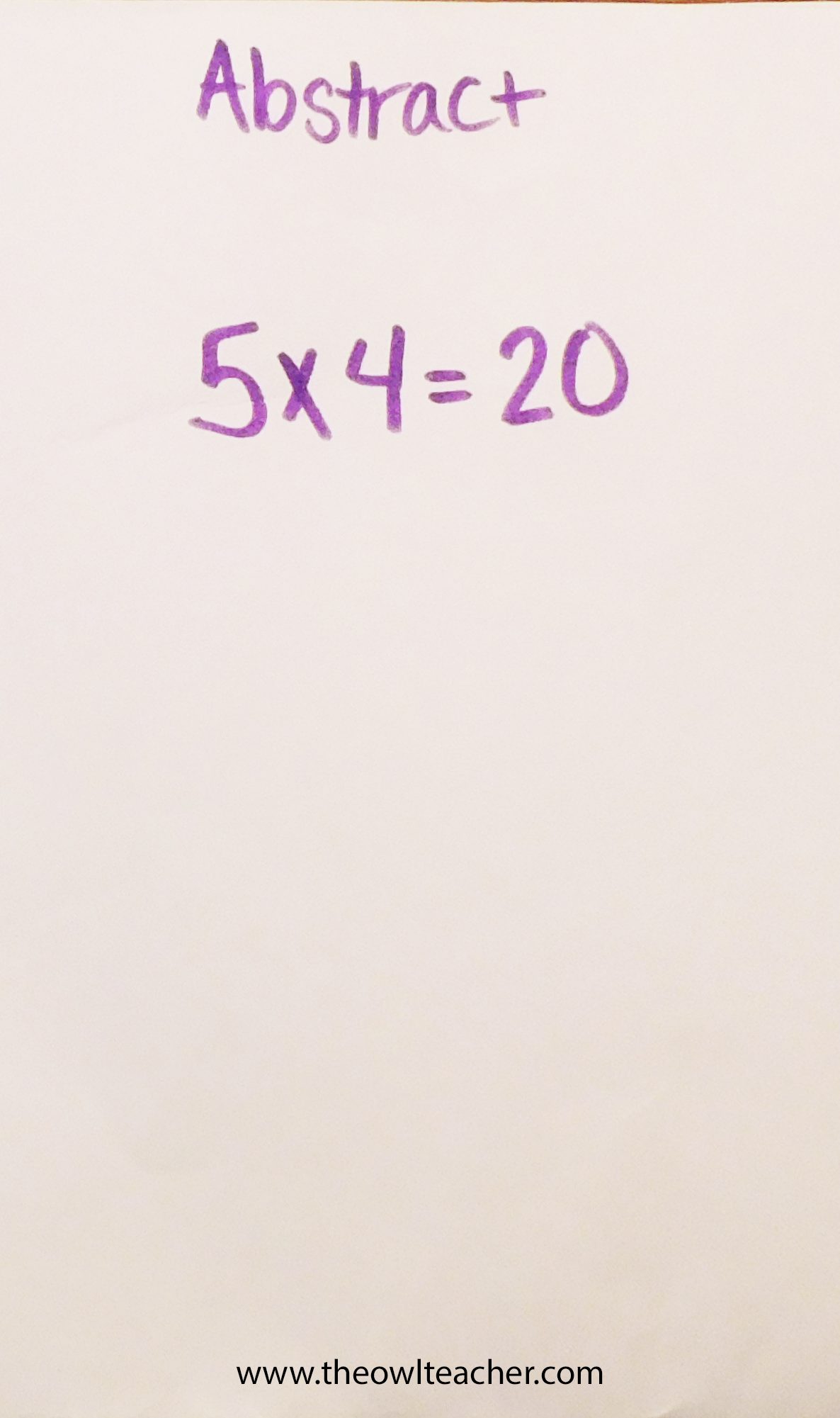
It has always amazed me how as we move up in the grade levels, we move more away from the concrete processes of mathematical concepts and into the abstract. I totally disagree with that methodology. Students, no matter the grade, need to “do” and “see” math concepts to truly grasp their meanings.
Finally, it’s critical that students have many opportunities to practice each process and demonstrate mastery before moving on to the next process for it to be successful.
With this methodology used with each math concept, students are sure to have a greater understanding and foundation of math.
Are you looking for math lessons that apply this methodology? Check out my Math Workshop Units.















One Response
Great read, thanks