Common Core requires that we teach students strategies before we introduce them to the traditional algorithms. When it comes to teaching multi-digit multiplication, it’s common for teachers to focus solely on the partial products method and forget about the rest. Instead, I like to scaffold my students’ learning first so that they are ready for both partial products and the traditional algorithm with more concrete methods.

It’s important that we are teaching students in the way that they learn best. One method of scaffolding is to start all concepts in a concrete manner and then work toward a more abstract manner. I talk about this in my post, Teaching Math so Students Get It. In this case of teaching my students how to multiply multi-digit numbers, I first start with the area model, then work up to the box model, introduce the distributive property, and then move into the partial products method. Depending on your grade level and standards, then you may teach the traditional algorithm after. This allows for scaffolding, instead of rescuing students later on.
The Area Model as a Multi-Digit Multiplication Strategy
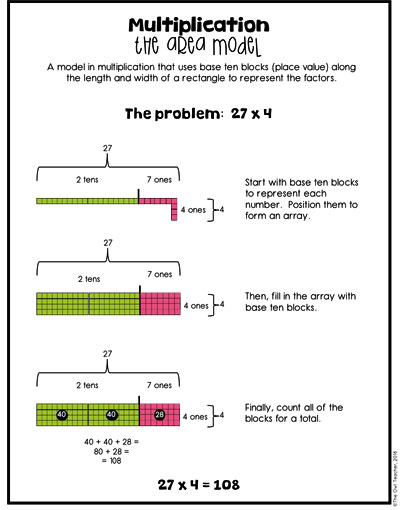
When I introduce my students to the area model, I first remind them of what this model looks like with basic multiplication numbers, such as 7 x 8. I provide students with base-ten blocks and have them create an array. Then I ask them to “just try” creating one with a larger number such as 27 x 4. Then, depending on how that goes, we will create the model. I will either model it or guide them. I remind students of place value and together we first create the sides of our array. For instance, in the problem 27 x 4, we create the two tens and the seven ones using our base ten blocks on one side and create the four ones on the other.
Next, we have to fill in the space to create an array. I express that we could do this with actual one base ten blocks, but it would take us a long time. Instead, it would be best to use the larger ones that would fit. This is an important step because later they will need this when they get to double digits and with understanding division. Once everything is filled in, we now count our total blocks for that section and add them up to get our final answer. You can see this in the anchor charts below, found in my fourth grade multi-digit multiplication math workshop unit (or found on TpT here).
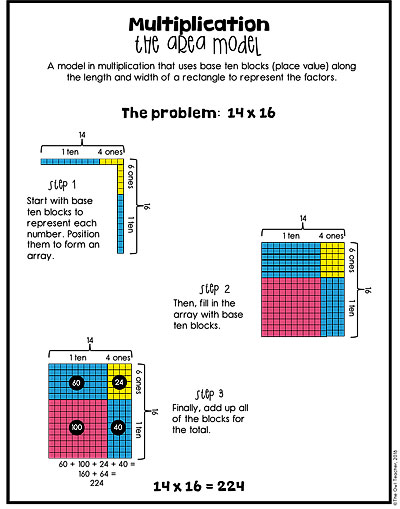
Using the area model with 2-digit numbers by 2-digit numbers is essentially the same, except the area model is just a bit larger. (I don’t recommend moving into the 2-digit by 2-digit model until after you have had plenty of practice with all of the multi-digit numbers by 1 digit. This post is to assist all multi-digit multiplication needs.) This area model typically involves more tens and hundreds.
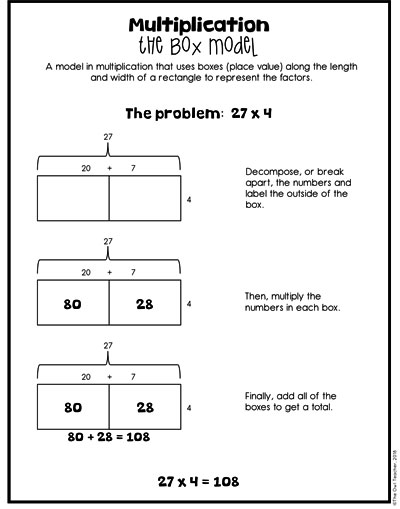
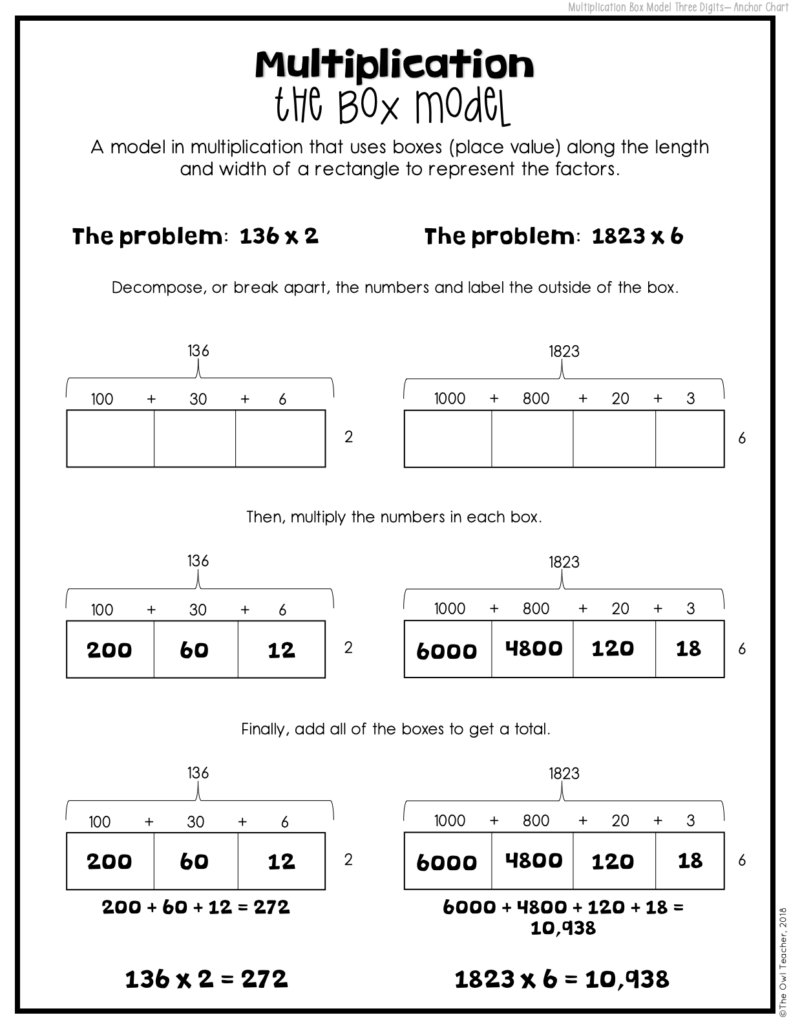
The Box Model as a Multi-Digit Multiplication Strategy
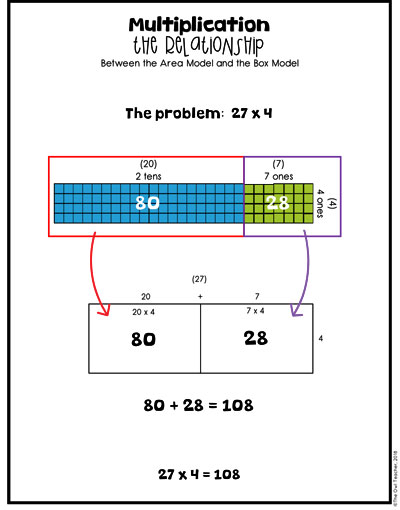
The box model follows the area model perfectly!
As seen in the image below, I typically create an area model first and then draw boxes around it to show my students the relationship between the two. Instead of actually usually manipulatives (concrete), we are now moving into drawing our models. In fact, in my math workshop and in my class, I often have my students draw symbols of the base-ten blocks after they have created the area model, so the transition is even nicer.
Now students are in the semi-concrete or representational stage. They are drawing the boxes and placing the numbers outside the box so that they can determine the answers for each box through multiplication.
The box model is really no different except that now they are not physically manipulating any base-ten blocks. This is a great time to mention decomposing, because that will be something you’ll be mentioning a lot during both the distributive property and later in other concepts, such as area.
When I talk about decomposing, I like to remind my students that this is really no different than what they did when they broke numbers up into the expanded form.
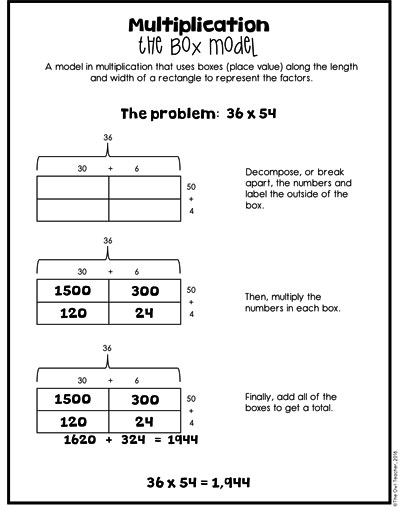
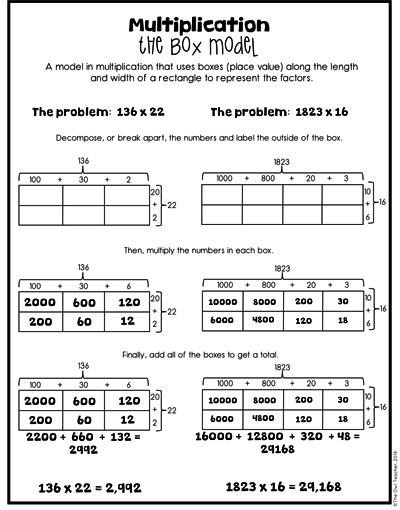
When students work on the 2-digit numbers by 2-digit numbers, they are now working with a 4-square box. Just as before, they are only multiplying the boxes in a grid-like way and then adding them up. See the charts below for a more detailed explanation.
The Distributive Model as a Multi-Digit Multiplication Strategy
For some reason, teachers don’t like to tackle the distributive property and/or the students fear it. But, if you have worked your way up using the previous methods, this strategy isn’t as scary as it appears.
Since we just talked about decomposing numbers in the last strategy, students should now know they can take the larger number and break it up into smaller numbers. I give them the freedom to choose how they break it up. Then I provide them with boxes to break it up and multiply away!
Down at the bottom of this distributive property chart (above), you can see that I have turned the box sideways and have used colored pens. I did this intentionally before I moved into partial products. I wanted to make sure students are seeing what each box is made up of. For instance, the first box (in red) is 100 x 6, the second box (in yellow-orange) is 20 x 6, and the third box is 3 x 6. Then I showed them how it’s written out and added up. I did this for two reasons. First, because they will see this again when we get to partial products (next), and second because they will see it when they learn to use the distributive property in algebra (FOIL) later.
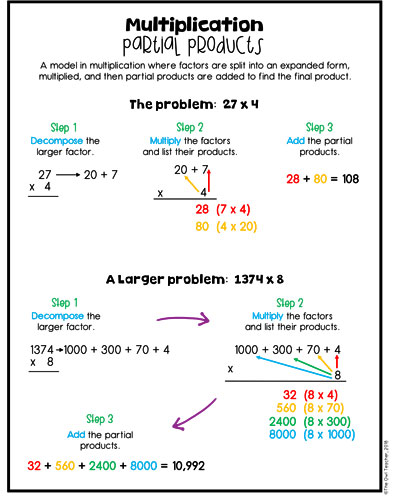
Partial Products as a Multi-Digit Multiplication Strategy
Most teachers are likely aware of the Partial Products method. In case you are not, it’s really just taking the larger number and breaking it out into expanded form and then having the other factor multiply each of the expanded form factors. Then they are added up to get the final product. (See chart below.)
You’ll notice that my colors are back. Whenever possible, I use colors to help differentiate each step. I remind students that we are using the distributive property (which is not scary now!) and decompose our larger number into the expanded form. Then we multiply each new factor one at a time. I always write each new product with the multiplication problem next to it so students can see where I got it from. Then, after we have found all the products to each of those, we add them up to find our final product. This strategy also helps later when introducing the “placeholder” in the traditional algorithm.
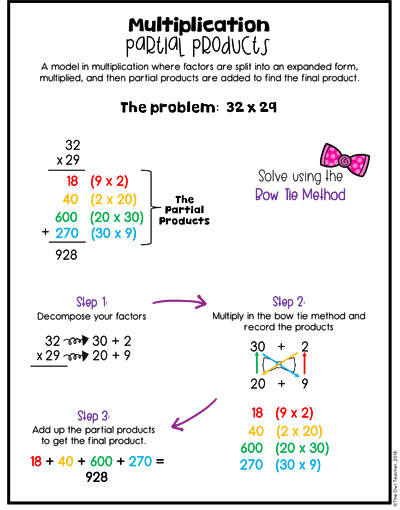
When we get to double digits, it is the same thing, but I like to introduce a method called the “bow tie method.” Just as before, students would decompose both factors into an expanded form. Then they multiply in a bow tie method. If you look at the illustration below, you can see this method through the use of the colors. I actually have my students draw it on their papers to help them so they don’t miss a factor as they are multiplying. As they work through the bow tie method, they record the products for each one. Once finished, they add the products together to get the final product.
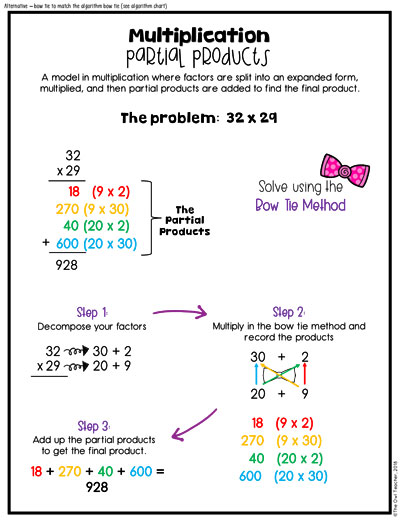
Understandably, if you prefer to have your students begin preparing for the traditional algorithm, you could have them do the “bow tie” method in the traditional algorithm motions, like in the chart below. Overall, the point of the “bow tie” method is to make sure no factors are missed or hit twice.
For students to truly be ready for multi-digit multiplication with the traditional algorithm, they must first go through the strategies that Common Core requires. This requires us to also teach in the way that students learn best. If you want your students to do well with multi-digit multiplication, you will need to scaffold the concepts by first starting with the concrete method of using an area model, working to a semi-concrete, representational model of the box method, and then into both the distributive property and the partial products method.
Using just one method will not cut it. Students need this gradual release with multi-digit multiplication before they’ll be ready or they just won’t fully understand the concept and be successful.
Grab the FREEBIE!
To help your students practice these strategies, I have a freebie to get you started! Click here to download the freebie!
Then check out my multi-digit multiplication lesson plans, games, and activities that go along with these anchor charts so that you can save time lesson planning today. Purchase the 4th grade Large Numbers Multiplication Math Workshop Unit here on my website or found on TpT by clicking here.