When Common Core stated that we needed to teach addition and subtraction strategies based on place value, properties of operations, and/or the relationship between addition and subtraction, I will admit I was at a loss for a long time. When I was growing up, the only thing I had learned was the standard algorithm. It was step-by-step do this, not that. Get it down, do it right! Over and over.
I had to do a lot of research to figure out what that standard was talking about. I’ll be honest: Since Common Core came out, I think I have done more research and critical thinking than in college AND than my own students! HA! (I kid…kind of.) But, I now understand, and I figured I could not have possibly been the only one with my head tilted like a cute doggy going, “Whaaaaaaaaaaat?”

Understanding the Standard for Addition and Subtraction Strategies
A while back I explained the differences between teaching the standard algorithm and teaching strategies in the classroom in my post, Which is Better in Math: Standard Algorithm or Invented Strategies? along with my opinion of which was better to implement. When I started researching actual strategies for addition and subtraction, I was stunned to find so many different types. Which strategies were best to teach my students? Which were easier for them to learn and manage?
According to the standards, I had to make sure students were using strategies that were based on place value, the properties of addition, and the relationship between addition and subtraction. I was finding strategies called expanded form, partial sums, decomposition, compensation, number line, split, shortcut, jump, counting on, counting back, and friendly numbers, just to name a few! And I’m sorry, but I didn’t have that much time to teach all those strategies in the classroom – and realistically, wouldn’t students get confused with too many?
I turned to my trusty friends John Van De Walle and Marilyn Burns. No, I’m not really friends with them, but I have many of their books, and I dug in deep. What did I find out? Those strategies above? They are all pretty much the same thing – synonyms. You’ll see. Read on.
The Addition and Subtraction Strategies
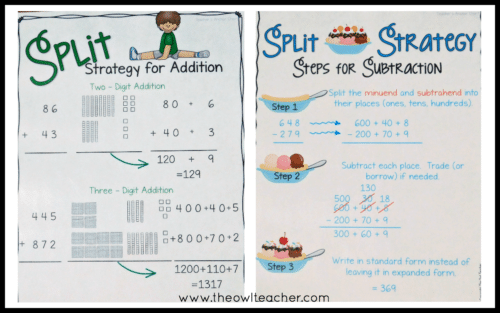
The Split Strategy (AKA: Partial Sums, Expanded Form, Decomposition): In this strategy, students are breaking apart a number based on its place value and then adding or subtracting each individual place to find the answer. Once each individual place is found, then the expanded form is returned back to the standard form.
The Jump Strategy (AKA: Counting On, Counting Back, Number Line): In this strategy students are using a number line to add or subtract. Students break their numbers up into friendlier numbers based on place value as they move along the number line to find the answer. What’s great about this strategy is that it is also based on the relationship between addition and subtraction (in the subtraction). If you look closely in the (poor quality?) image below, I demonstrate this by making my students think of the inverse operation of 287 + ____ = 524. That is basing it on the relationship. I love when I hit two at once!

The Shortcut Strategy (AKA: Friendly Numbers, Compensation): In this strategy students are changing one of the numbers to a friendlier number by adding to it. In addition, a friendly number is a multiple of 10. In subtraction, a friendly number is one that ends in 9. Then, students change the bottom number according to the strategy and then finish the operation with the new set of numbers. This is also based on place value. Of the three strategies, this one can be the trickiest, because it is different between addition and subtraction.

When we think about the properties of addition, Common Core is referring mostly to the commutative property, where students remind themselves, for example, if they know that 10 + 80 is 90, then 80 + 10 is also 90.
Through all my research, I came to realize that it was not about a specific strategy that students had to learn but rather how to use strategies and to rely on them, instead of simply using memorization and algorithms to arrive at an answer. Students need to understand that with mathematics there is more than one way to solve an equation. Mathematicians utilize methods that are most meaningful, efficient, and faster for them – whether that is through the use of an algorithm or an alternative strategy. Strategies are often meaningful to those who use them and are often faster and less susceptible to error.
When you are teaching addition and subtraction strategies, remind yourself that you are not teaching each of these strategies to mastery but instead are providing tools for the student to try and to find which works best for him or her. When assessing students, instead you should be providing them with an addition or subtraction problem and asking the student to solve it using at least two different approaches. Then, students should explain their thinking using mathematical vocabulary and by showing their work through the use of numbers and pictures.
My hope is that this (long!) post has helped you understand the addition and subtraction strategies a bit more and removed any frustration they may have caused you. Now head over to my Teaching Addition and Subtraction Strategies blog post to learn how I teach each of these strategies in my classroom. You can also get a freebie!